Number 7
What is the missing length of the leg for each triangle? Give your answer to the nearest tenth of a millimetre.
a)
a²+b²=c²
a²+5²=9²
a²+(5x5)=(9x9)
a²+25-25=81-25
a²=56 mm²
√a²=√56 mm²
√a²=√56 mm²
a=7.5 mm
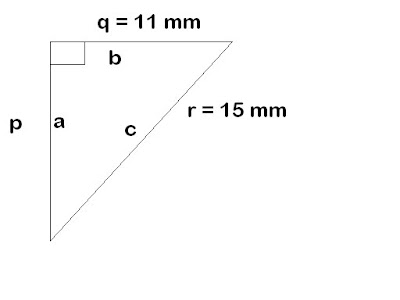
b)
a²+b²=c²
a²+11²=15²
a²+(11x11)=(15x15)
a²+121-121=225-121
a²=104 mm²
√a²=√104
a=10.2 mm
Number 10
What is the minimum distance the player at third base has to throw to get the runner out at first base? Express your answer to the nearest tenth of a metre.

a²+b²=c²
27²+27²=c²
(27x27)+(27x27)=c²
729m²+729m²=c²
1458m²=c²
√1458=√c²
38.2m=c
The player must throw a distance of 38.2 metres.
Number 13
Determine the length of the base of the large triangle. Express your answer to the nearest tenth of a millimetre.
a²+b²=c²
8²+b²=10²
8²+b²=10²
(8x8)+b²=(10x10)
64-64+b²=100-64
64-64+b²=100-64
b²=36mm²
√b²=√36
b=6mm
b(2)=6(2)
Base=12cm
Number 16
The deadly number 16. Hopefully you won't need this guide, as it is for people who have been reduced to tears (not literally) by this question. But if you are one of these people, you are welcome to look at the answer.
What is the length of the red diagonal in the box? Express your answer to the nearest tenth of a millimetre.

Now, imagine that the triangle has been cut in half, from the top right corner to the bottom left corner, so that the diagonal is on a 'flat surface'. Using the height (5mm) and length (12mm), we can find the hypotenuse of the 'triangle' that was created when the rectangle was cut in half, using the Pythagorean theorem (height-a, length-b):
a²+b²=c²
5²+12²=c²
(5x5)+(12x12)=c²
25+144=c²
169cm²=c²
√169=√c²
13mm=c
After that, imagine turning the triangle so that you can see the red diagonal cutting a rectangle in half. You have already found the bottom of the rectangle (13mm), and you have the measurements for the right side of the rectangle, the width (7mm). Using the Pythagorean theorem, you can now find the red diagonal (width-a, bottom-b).
a²+b²=c²After that, imagine turning the triangle so that you can see the red diagonal cutting a rectangle in half. You have already found the bottom of the rectangle (13mm), and you have the measurements for the right side of the rectangle, the width (7mm). Using the Pythagorean theorem, you can now find the red diagonal (width-a, bottom-b).
7²+13²=c²
(7x7)+(13x13)=c²
49+169=c²
218cm²=c²
√218=√c²
14.8cm=c
Hopefully, you found that helpful. Good night (it's 1:05 AM), and goodbye.


Great job Meldrick! Your images were very helpful and easy to understand. I like how you added some color. I like how you really explained question 16. It's pretty amazing how you solved number 16! Keep up the good work!
ReplyDeleteGreat job Meldrick! I like how you changed the color of the important words. I found a mistake, on #16 you mixed up some of the measurements. You put "cm" when its suppose to be "mm". Overall good job!
ReplyDeleteGood Job Meldrick! I like your post, its simple. For number 16 I kind of did the same thing, but I explained mine with pictures. Awesome job. :)
ReplyDeleteGood job Meldrick! Your post was very simple and organized which made it easy to read. I really liked the pictures and you explained number 16 really well. Next time try to add a link and video. Otherwise, great job!!
ReplyDelete