Surface Area Quiz Answers

Here is a link.

Cylinder Volume and Volume Problems
Example from 7.3:

Example from 7.4:

Anna's Surface Area

Finding the surface area of Rectangular Prism and Triangular Prism.

Triangular Prism



































Rectangular Prism.



















Cylinder Volume and Volume Problems

7.3 question

v= π . r^2 . h
v= (3.14 x 5 x 5)x23cm
v=78.5 x 23cm
v= 1805.5 cm^3












7.4 question




a) Yes, he has enough small triangular Prisms to make a giant prism with a base of 5.6m and height of 6.8m.

b) v=b.h^1/2.h^2

v=(5.6x1.18)x6.8 m

v= 10.08 x 6.8 m

v= 69 m^3

The Volume of the new prism is 69m^3

Hendrik's daily question #3

Hello my fans and people who r just browsing the web Fridays question was If you were to have one of these super powers what would it be? 25 % voted to control who smells your farts and 75% to control time. Now I want you to tell people to watch out for my blogs tell all your friends to submit tell your friends,your brothers/siblings, and if you got one of those fancy new dogs tell them to also If you have any request for a question leave it in the comment section i promise you I will look at all of them and good ones or crazy ones will get chosen. Today many people have told me that i will get in trouble so here is today's question.Remember I make these at lunch so I do not no the result yet and if you ever want to see me make them I will be in Mr.Harbeck's math lab.

How bad do you think I got/gonna get in trouble?

Mr.Harbeck liked them and told me it's OK

He didn't care

He told me to stop

he yelled at me

I got suspended

I got expelled

I was never to be seen again (gulp)

or View Results

Create your own poll at Flisti.com

Hendrik's daily question #2

yesterdays question was if u would appreciate daily questions 4 voted yes 1 no the other options weren't chosen so here is today's question:

If you were to have one of these super powers what would it be?

control who smells your farts

control time

x-ray vision

fly

mind control

or View Results

Create your own poll at Flisti.com

Homework Book Pg 54-55

Choose 3 questions from pages 54 and 55

2. Calculate the surface area of each rectangular

prism to the nearest tenth of a centimeter squared.

length x width = a

S- 5 x 3.2 = 16 cm2

- 5 x 3.2 = 16 cm2

F- 11.5 x 5 = 57.5 cm2

- 11.5 x 5 = 57.5 cm2

T- 11.5 x 3.2 = 36.8 cm2

- 11.5 x 3.2 = 36.8 cm2

________________________________

Total Surface Area =220.6 cm2

length x width = a

F- 12 x 10.4 = 124.8 cm2

- 12 x 10.4 = 124.8 cm2

T- 10.4 x 4.5 = 46.8 cm2

- 10.4 x 4.5 = 46.8 cm2

S- 12 x 4.5 = 54 cm2

- 12 x 4.5 = 54 cm2

________________________

Total Surface Area = 451.2 cm2

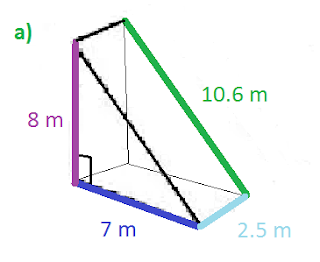
3. Find the surface area of each triangular

prism to the nearest tenth of a meter squared.

a of a triangle = base x height divided by 2

a of rectangle = length x width

8 x 2.5 = 20 m2

10.6 x 2.5 = 26.5 m2

2.5 x 7m = 17.5 m2

7 x 8 = 56/2 = 28 m2

7 x 8 = 56/2 = 28 m2

___________________

Total Surface Area = 120 m2

a of a triangle = base x height divided by 2

a of rectangle = length x width

8 x 4.5 = 36 m2

8 x 4.5 = 36 m2

8 x 6 = 48 m2

6 x 3.35 = 20.1/2 = 10.5

6 x 3.35 = 20.1/2 = 10.5

_____________________

Total Surface Area = 140.1 m2

4. Ty is painting this storage bench for the deck.

How much area does he need to paint, to the nearest

hundredth of a square meter?

length x width = a

S- 0.38 x 0.5 = 0.19 m2

- 0.38 x 0.5 = 0.19 m2

F- 0.5 x 1.56 = 0.78 m2

- 0.5 x 1.56 = 0.78 m2

T- 1.56 x 0.38 = 0.5928 m2

- 1.56 x 0.38 = 0.5928 m2

________________________

= 3.1256 round up...

Total Surface Area = 3.13 m2

Cylinder Volume and Volume Problems




r = d / 2…………………….v = π.r.r.h asdfghjkl;………….502.4m3^ / 2 = 251.2m3^
r = 8 /2……………………..v = (3.14 x 4 x 4) x 10
r = 4m……………………….v = 50.24 m2^ x 10m
…….asdfghjkl;…………….v = 502.4 m3^





r = d / 2.......................v = π.r.r.h

r = 80 / 2……………….v = (3.14 x 40 x 40) x 45

r = 40cm……..….……..v = 5024 cm2^ x 45cm
……………………………..v = 226,080cm3^

226,080 / 80 = 2826cm2^

2826 / 3.14 = 900cm

√900 = 30cm

30 x 2 = 60cm -diameter

Breanna's Homework Book Pg.54-55

These are the 3 questions I did in our homework booklet.

Question #2

Calculate the serface are of each rectangular prism to the nearest tenth of a centimetre squared.

a)

LxW

11.5 x 3.2 = 36.8

11.5 x 3.2 = 36.8

11.5 x 5 = 57.5

11.5 x 5 = 57.5

3.2 x 5 = 16

3.2 x 5 = 16

36.8 + 57.5 + 16 = 110.3

110.3 x 2 = 220.6

T.S.A = 220.6

b)

LxW

12 x 10.4 = 124.8

12 x 10.4 = 124.8

12 x 4.5 = 54

12 x 4.5 = 54

10.4 x 4.5 = 46.8

10.4 x 4.5 = 46.8

124.8 + 54 + 46.8 = 225.6

225.6 x 2 = 451.2

T.S.A = 451.2

Question #3

Find the surface area of each triangular prism to the nearest tenth of a centimetre squared.

a)

LxW/2 LxW

7 x 2.5 = 17.5

8 x 2.5 = 20

10.6 x 2.5 = 26.5

8 x 7 = 56 /2 = 28

8 x 7 = 56 /2 = 28

17.5 + 20 + 26.5 + 28 +28 = 120

T.S.A = 120 cm squared.

b)

L x W/2 L x W

8 x 4.5 = 36

8 x 4.5 = 36

8 x 4.5 = 36

3.35 x 6 = 20.1 /2 = 10.05

3.35 x 6 = 20.1 /2 = 10.05

36 + 36 + 36 + 10.05 + 10.05 =128.1

T.S.A = 128.1

Question #4

Ty is painting this storage bench for the deck. How much area does he need to paint, to the nearest hundreth of a square metre?

LxW

0.5 x 1.56 = 0.78

0.5 x 1.56 = 0.78

0.5 x 1.56 = 0.78

0.5 x 1.56 = 0.78

0.5 x 0.38 = 0.19

0.5 x 0.38 = 0.19

0.78 x 4 = 3.12

0.19 x 2 = 0.38

0.38 + 3.12 =

T.S.A = _______

Here is a link that I found! *click here*

Also Here`s a video I found! Check it out

What is the answer to question #4?

35

350

3.5

0.35

or View Results

Create your own poll at Flisti.com

Textbook pg. 180-181

Question 8,16

8.Paco builds a glass greenhouse.

a) How many glass faces does the greenhouse have?
b) How much glass does Paco need to buy?

Shelby wants to paint the walls and ceiling of a rectangular room.

Type of paint Size of paint can Cost
Wall paint 4L $24.95
1L $7.99
Ceiling paint 4L $32.95

One liter of paint overs 9.5 m square?
a) what is the least amount of paint shelby can buy?
b) how much will it cost with tax?

Hendriks Daily questions #1

To all who might care I Hendrik room 873 will be doing a daily question each school day starting now so today's question is:

Would you appreciate having these pols about none sense every school day

Yes

No

Maybe

I don't care

Not EVERY school day

I really don't care

If u think I'm going to look at them u r greatly mistaken

or View Results

Create your own poll at Flisti.com

Volume Post

a)v=π.r.r.h
v=3.14cmx5cmx5cmx23cm
v=78.5cmx25cm
v=1806.5cm^3
b)v=π.r.r.h
v=3.14cmx14cmx14cmx12cm
v=615.44cmx12cm
v=7385.28cm^3
c)v=π.r.r.h
v=3.14cmx0.5cmx0.5cmx1.5cm
v=12.75cmx1.5cm
v=19.125cm^3



R=D/2
D=o.8cm
0.8cm/2=R
R=0.4cm^3

V=π.r.r.h
V=3.14mx0.4mx0.4mx10m
V=0.5024mx10
V=5.024m^3




Questions: 3,5,7,11




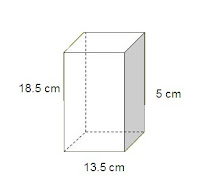
3.Find the surface area to this rectangular prism to the nearest tenth of a cm.
Answer:819.5 cm













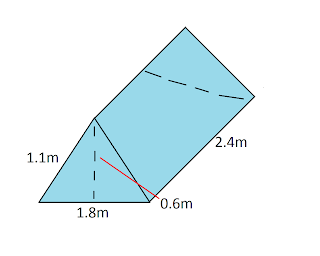
5.Calculate the surface area of this ramp in the shape of a right triangular prism. Give your answer to the nearest tenth of a square metre.
Answer:23.8 cm













7.Given the area of each face of a right rectangular prism, what is the surface area?
Answer:94 mm











11.Dallas wants to paint three cubes. The cubes measure 1 m × 1 m × 1 m, 2 m × 2 m × 2 m, and 3 m × 3 m × 3 m, respectively. What total surface area will Dallas paint if he decides not to paint the bottoms of the three cubes?

70 m

0.7 m

3

-1

or View Results

Create your own poll at Flisti.com

Answer:70 m

How to find surface area of rectangular prism.
eg:









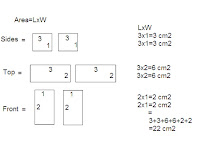
How to find the surface area of a triangular prism
eg:

Mussie Final Percent Post

1. The front wheel of a tricycle is 155% as large as its rear wheels. Use hundred grids to show how the front wheel compares to the rear wheels.

2. The cost for a downloaded game was $10.99. Added to this cost was a 10% before tax processing fee, 5%GST and 7%PST. What is the total cost of the game?

3. The number of caribou in a particular herd was monitored over a two-year period. The first year, the size of the herd was estimated at 30 000. The second year, the herd was estimated to be 90% of its original size. What was the approximate size of the herd in the second year?

4. What is a better deal:
a) 60% off a pair of shoes
b) 20% off a pair of shoes then a 40% reduction of the discounted price.
Use an example to show that your thinking.

Pg.180 Nr.2 4 6 8

2A rectangular prism has six faces why might you have to find the surface for only 3 of hose faces: because the other 3 are the same so u just have to times the other ones by two.

4you times all sides by each other then you add the results

6 to find the area of this triangle 9.1x4.5/2=20.475x2=40.95
3x9.1=27.3
6.4x3=19.2x2=38.4
If you add all the answers together you will get the surface are of your triangle

8 for a you just count all the faces and for b you 180x60=10800cm=108m/2x2=108
1.1mx2.4m=2.64x2=5.28
1.8x2.4=4.32
then you add all of the answers together and you get your answer

Where is Mr.Harbeck

He was abducted by Aliens

Hes sick

He is skiping

He is going through a veryyyyyyyyyyyyyy long tunnel and therefore cant phone anybody

He is eating cheetos and fried chicken while watching the comedy network

He is stuck in the snow

or View Results

Create your own poll at Flisti.com

Surface Area Questions

4x5=20

4x6=24

4x6=24

=68

5/2=2.5

2.5x7=17.5

2.5x7=17.5

17.5+17.5=35

Here is a link to help you understand.

What is the answer?

103

403

203

i don't care

or View Results

Create your own poll at Flisti.com

Cylinder Volume and Volume Problems



πr^2
3.14x5cmx5cm
a= 78.5cm^2
Area of base X height
78.5cm^2 X 23cm
v= 1805.5 cm^3

Christian's Final Percent Post

1. The front wheel of a tricycle is 155% as large as its rear wheels. Use hundred grids to show how the front wheel compares to the rear wheels.

2. The cost of a downloaded game is 10.99. Added to this cost was a 10% before tax processing fee, 5%GST and 7%PST. What is the total cost of the game?

3. The number of caribou in a particular herd was monitored over a two-year period. The first year, the size of the herd was estimated at 30 000. The second year, the heard was estimated to be to be 90% of its original size. What was the approximate size of the herd in the second year?

4. What is a better deal:
a) 60% off a pair of shoes
b) 20% off a pair of shoes then a 40% reduction off the discounted price.
Use an example to show your thinking.

*The questions in the video aren't in order to the blog. Sorry.

Mussie's Surface Area Scribe Post,volume

Here are the two rectangular prisms. Please find the Total Surface area using a net and by using the Top, Front and Side views of the prism.


The lengths of a rectangular prisms are 4 cm and 8 cm and 1 cm. What is its Total Surface Area?
A=LxW

8x4=32

1x4=4

1x8=8

A=32+4+8=44

A=44*2=88cm^2

The lengths of a rectangular prism are 2 cm and 6 cm and 2 cm. What is its Total Surface Area?

A=LxW

2x6=12

6x2=12

2x2=4

A=12+12+4=28

A=28x2=56cm^2

link

pi x r x r x h

3.14 x 5 x 5
78.5x23cm
v=1805.5cm^3



















Yes he has enough
1.18x5.61/2=3304
3304m^2x6.8=22467.2
v=22467.2

Final Percent Post

To Finish of percents we were required to do a percent video to these following questions:

1. The front wheel of a tricycle is 155% as large as its rear wheels. Use hundred grids to show how the front wheel compares to the rear wheels.

2. The cost for a downloaded game was $10.99. Added to this cost was a 10% before tax processing fee, 5%GST and 7%PST. What is the total cost of the game?

3. The number of caribou in a particular herd was monitored over a two-year period. The first year, the size of the herd was estimated at 30 000. The second year, the herd was estimated to be 90% of its original size. What was the approximate size of the herd in the second year?

4. What is a better deal:
a) 60% off a pair of shoes
b) 20% off a pair of shoes then a 40% reduction of the discounted price.
Use an example to show that your thinking.

The video and answers are as follows:

Final Percent Post

Percents
This chapter, we learned about percent. Percent means out of 100. Percents can be converted into fractions and/or decimals.
Example: 75% - 75/100 or 0.75

Representing Percents
Percents can be represented on a hundred grid.
Example: 55%

Fractions, Decimals and Percents
Percents can be represented as a fraction or a decimal. Example: 50% ; 50/100 ; 0.5

Percent of a number
You can find percent of numbers by using mental math strategies. They are halving, doubling, a dividing by 10. Example: 50% of 1000 is 500

Combining Percents
Combine percents by adding to solve the problems. Example: 5% + 7% = 12%

Here is my percent video.

Final Percent Post

What is a Percent??

• A percent is a number out of one hundred.

4.1 Representing Percents

• To represent a percent you can use a hundred grid
• If all of the squares are coloured in then that is 100%
• To represent a fractional percent in between 0 and 1% you colour in part of one little square

4.2 Fractions, Decimals, and Percents

• Fractions decimals and percents can be used to represent numbers
• Percents can be shown as a......
• Fractions or a
• Decimals
• (example) 250% = 250 /100

4.3 Percent of a Number

• You can use mental math stratagies such as doubling, halving, doubling or dividing by ten to find the percent of some numbers.

4.4 Combining Percents

• To solve problems like this you can do that by adding
• a good example is 5% + 7% = 12%
• Percents can be used to determine the amounts that result from consecutive percents increasing or decreasing

Here is a website about percents.

Here is the video I created.

Hope it helps! (:

Final Percent Post

1. Percent - means out of 100 and it can be shown as decimals and fractions.

For example 80% can be 0.8 and 8/10.

Representing Percents;

You can represent a percent by using a grid.

For example 20% can be shown like this.

Percents can also be shown as decimals and percents. For example 50% can be 0.5 or 1/2.

Percent of a Number
You can use mental math strategies like halving, doubling, and dividing by 10 to find a percent of a number. You can also write the percent as a decimal then multiply it by the number.
For example,
12 1/2 % of 50 = 0.125 x 50 12 1/2% = 12.5%
= 6.25 = 0.125

Combining Percent

You can combine Percents to solve a problem.

For example if your buying a bike for $100 and the tax is 5% PST and 7% GST = 12%.

You can find the answer buy finding 1% of $100 then multiply by 12 to find how much the tax would be with the original price. So 100 divided by 100 = 1 then multiply by 12 and you will find the tax which is $12. All together you are paying $112 for the bike.

2. Will upload later on having some problems with it.

3. I didn't have a percent scribe post.

4. A link to a website about percents.

http://www.aaaknow.com/pct.htm

Final Percent Post

Percent:


Means it's out of a hundred or another name for hundredths, it can also be represent as a decimal or as a fraction.


Ex. 50% means 50 out of 100 or 50/100 or 0.65


Representing Percent


A percent can be represented on a hundred grid.
ex. 20%


































Decimals, Fractions, and Percents

Percents can be written as a decimal or a fraction.

ex. 1/2=50% 25%=0.25



Percent of a Number

You can use mental math strategies such as doubling, halving, and dividing by ten to find the percent of some numbers.

ex. 12 1/2 of 50%= 0.125x 50= 6.25



Combining Percents

Percents can be combined by adding to solve problems.
ex. 3%+5%=7%



You can add the combined percent amount to the original number to find the increase in a number.

ex. 10% of 100= 0.10 x 100=10 100+10= 110



You can multiply the original number by a single percent greater than 100.

ex. 110% of 100 = 1.10x 100 = 110



Percents of percents can be used to determine amounts that result from consecutive percent increases or decreases.








Here's my percent video :D


Click here to go to a site that will hopefully help you understand more about percents.

Final Percent Post

Percent means out of one hundred. It's also known as hundredths. It can be represented by decimals and fractions.
Representing Percents
You can represent percents by showing it on a hundred grid.

Fractions, Decimals, Percents

Percents can be written as decimals, and fractions.

Percent of a Number

To find a percent of a number, you can use mental math strategies such as, halving, doubling, and dividing by 10. Another way is to write the percent as a decimal and multiply it by the number.

I didn't have a scribe post for percents.
Here is a link to a website about percents.
This is another link to a percent website.