For this scribe i had to answer questions 18,20 and 22. Enjoy!
18. The question says if the square floor mat has a side length of 14m, what is the area of the square floor mat in square meters?
Here is my answer:
A=S2
A=142
A=14x14
The area is 196 m2.
20. This questions says that Adams uncle has instructions for building a shed, a page of the insturtions was not as clear as he thought.
a) The question asks for the area of the rectanlge. Here is what i did:
A= LxW
A= 9x4
A= 36m2
The area is 36m2.
b) Now this time is ask`s for the side length of the square, and this is what i tohught of.
I think that the answer will be 6 because when you square 6 it equals 36.
Ex. 2
6 = 36 or 6x6= 36.
22. This question ask for three questions that are connected to to the largest in Beijing that has an area of 396,900 m squared.
a) This question is asking about what the dimenstions on the square are. This is what i did.
630 m by 630 m
=630m squared = 369,000
The answer is 369,000.
b) This question asks if the dimention would be 629 m by 629 m, what would be the answer? I did this.
629 m by 629 m
= 629 squared = 395, 641.
The answer is 395,641.
c) This question is asking if the area is less than 394, 000 but greater than 386,000, what would the dimention between those numbers? I answered like this.
622 squared = 386,884
623 squared = 388,129
624 squared = 389,376
625 squared = 390 625
626 squared = 391,876
627 squared = 393,129
Those are all the whole possible dimensions that I could have.
Here is a link on finding the area of a square or rectangle.
http://http//http//www.ehow.com/how_2256131_calculate-area-square-rectangle.html
and here is a video.
This is a place for the community of learners in Room 8-73 to learn and enjoy math. It is an extension of the classroom making it accessible 24 hours a day, 7 days a week.
Sunday, October 31, 2010
Breanna- Scribe 5
Scribe 6 - 2 Questions From Page 87
In this scribe, I had to pick two questions on page 87 and answer them. These are the two questions I decided to answer:
24. a) What are the next three triangular numbers
10, 15, 21
b) Add together any two consecutive triangular numbers. What do you notice about the sums?
The sums equal perfect squares.
Example, 1+3=4 3+6=9 6+10=16
25. A square digital photo on the computer has an area of 144 cm2.
a) What is the side length of the photo?
 The side length of the photo is 12 cm.
The side length of the photo is 12 cm.b) The photo is enlarged so that the side length is now 36 cm. What is the area of the enlarged photo?
 The area of the enlarged photo is now 1296 cm2
The area of the enlarged photo is now 1296 cm2c) How many times as large as the original area is the enlarged area?
1296/144=9 The original photos area was enlarged by 9x
d) How many times as large as the original side length is the enlarged side length?
36/12=3 The original photos side length was enlarged by 3x
e) Use what you know about the square root of a perfect square to identify the relationship between the numbers in parts c) and d).

Saturday, October 30, 2010
Scribe Post #3
Show you Know Page 84




Determine the side length of a square with the area of 196cm2.
Prime Factorization:
196cm2 = area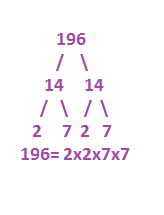
14cm = side length
Side length = Square root
Square root is the number that
multiplied itself equals the
number you are looking for.
196 divided by 14 = 14
14 x 14 = 196
Questions from the text book:
3. The factors of 36 are 1, 2, 3, 4, 6, 9, 12, 18, and 36. Use words and/or
diagrams to explain how you know which factor is the square root of 36.

6 is the square root of 36 because 6 is the number that multiplied by itself you get the number your looking for.
7. Determine the prime factorization for each number:
a) Not a perfect square b) Not a perfect square


c) A perfect square

12. Determine the square of each number:
The square of a number is the area.
To get the area of a square you have
to multiply side x side.
a) 3 = side
area = side x side
area = 3 x3
area = 9
b) 18 = side
area = side x side
area = 18 x 18
area = 324
14.Determine the side length for a square with an area of 900cm2.

area = side x side
area = 30 x 30
area = 900cm2
The side length of the square is 30cm2.
Scribe 4
17. A fridge magnet has an area of 54 mm 2. Is 54 a perfect square? Use prime factorization to find the answer.
54=2x3x3x3, No 54 is not a perfect square, its an odd number- factors 2 and 3
19.The gym teacher told the students to run twice around the perimeter of the school field. The area of the square field is 28 900 m 2. What distance did the students run?
1360 m
21.Kate wants to put a patio in her backyard. the patio stones each have an area of 1m 2. she created the rectangular design shown.
 A) What is the area of the patio?
A) What is the area of the patio?
B) What are the 5 dimensions of another
rectangular patio she could build
with the same area?
C) Kate decides to make a patio with the
same area but she wants it to be a square
with whole number side lengths. Is this
possible? Explain your reasoning.
A) 56 m 2
B) 7m- 8m This is one set of dimensions for the patio.
C) No its not possible cause 56 is not a perfect square.

54=2x3x3x3, No 54 is not a perfect square, its an odd number- factors 2 and 3
19.The gym teacher told the students to run twice around the perimeter of the school field. The area of the square field is 28 900 m 2. What distance did the students run?
1360 m
21.Kate wants to put a patio in her backyard. the patio stones each have an area of 1m 2. she created the rectangular design shown.
 A) What is the area of the patio?
A) What is the area of the patio?B) What are the 5 dimensions of another
rectangular patio she could build
with the same area?
C) Kate decides to make a patio with the
same area but she wants it to be a square
with whole number side lengths. Is this
possible? Explain your reasoning.
A) 56 m 2
B) 7m- 8m This is one set of dimensions for the patio.
C) No its not possible cause 56 is not a perfect square.

Friday, October 29, 2010
olivia Thomas rates ratios proportional reasoning
rates - compares two quinities measured in different units.
Eg. $1.69 per 100g for purchasing bulk food.
72 beats per minute is a heart rate.
ratios- Compares two quantities measured in the same units.
two term ratios eg. a:b or a to b
three-term ratio eg.a:b:c or a to b to c
proportional reasoning- A reletionship that says that two ratios or two rates are equal.
can be written in fraction form 2km/3h , 6km/9h
Eg. $1.69 per 100g for purchasing bulk food.
72 beats per minute is a heart rate.
ratios- Compares two quantities measured in the same units.
two term ratios eg. a:b or a to b
three-term ratio eg.a:b:c or a to b to c
proportional reasoning- A reletionship that says that two ratios or two rates are equal.
can be written in fraction form 2km/3h , 6km/9h
I like math because i like to learn math so i can be in grade nine.
I was not here for grade 7.
I want to learn about math because i like math.
I'm in grade i wasn't here for grade 7 im new here
I was not here for grade 7.
I want to learn about math because i like math.
I'm in grade i wasn't here for grade 7 im new here
Hi my name is kyle I'm a math student in grade eight when people ask me if I like math I say sometimes I do good sometimes I do bad that's because I sometimes a little thing can catch my attention.
In grade 7 I was not the beast student in MR.Isfelds class I was almost never listened to him.
To be a better student i need to focus more on my subjects like math and L.A. and more.
I never did a post in grade 7.
In grade 7 I was not the beast student in MR.Isfelds class I was almost never listened to him.
To be a better student i need to focus more on my subjects like math and L.A. and more.
I never did a post in grade 7.
Krizna's Sesame Video Post
Group Members:Jennily and Krizna
Rate:Compares two quantities measured by different units.
Two Term Ratios:Compares two quantities measured in the same units.
Three term ratios;compare three quantities measured in the same units.
Part to Part ratios:Compares diffrent parts of group to each other.
Part to Whole Ratios :Compares One part of a group to the whole group.
Unit Rate:A rate in which the second term is one.
Unit Price:A unit rate used wen shopping
Rate:Compares two quantities measured by different units.
Two Term Ratios:Compares two quantities measured in the same units.
Three term ratios;compare three quantities measured in the same units.
Part to Part ratios:Compares diffrent parts of group to each other.
Part to Whole Ratios :Compares One part of a group to the whole group.
Unit Rate:A rate in which the second term is one.
Unit Price:A unit rate used wen shopping
Scribe 2- Square Numbers
Show You Know- Pg.83:
Determine the area of a square with a side length of 16mm.
Answer: 256mm2
How: I multiplied or squared 16 by itself so it looks like this:
16x2 or 162 =265m2
Page 85 Questions 2, 6, 11, 15
2)How would you use prime factorization to determine the square root of 225? Compare your answer with a classmate's.
You would make a tree that had 225 on top of the tree then from there you divide until you get prime numbers.
6) a: 64
/ \
8 x 8
/ \ / \
4x2 x 4x2
b: Yes because the side are equal.
c:

11) What is the square of each number?
a: 9- 9x9= 81
b: 11- 11x11= 121
15) Evaluate. -- Definition of Evaluate:
to ascertain the numerical value
a)

b)

c)

Click here for a math site that will help you in square roots and squares.
Here is a video that will help you in square rooting.
Here is a picture displaying an example of prime factorization.

Determine the area of a square with a side length of 16mm.
Answer: 256mm2
How: I multiplied or squared 16 by itself so it looks like this:
16x2 or 162 =265m2
Page 85 Questions 2, 6, 11, 15
2)How would you use prime factorization to determine the square root of 225? Compare your answer with a classmate's.
You would make a tree that had 225 on top of the tree then from there you divide until you get prime numbers.
6) a: 64
/ \
8 x 8
/ \ / \
4x2 x 4x2
b: Yes because the side are equal.
c:

11) What is the square of each number?
a: 9- 9x9= 81
b: 11- 11x11= 121
15) Evaluate. -- Definition of Evaluate:
to ascertain the numerical value
a)

b)

c)

Click here for a math site that will help you in square roots and squares.
Here is a video that will help you in square rooting.
Here is a picture displaying an example of prime factorization.

Mussie Sesame street video
Rate: compares two quantities measured in the same units
Two Term Ratio: compares two quantities measured in the same units
Three Term Ratio: compares three quantities measured in the same units
Part to Part Ratio: compares different parts of a group to each other
Part to Whole Ratio: compares on part of a group to the whole group
Unit Rate: a rate in which the second term is one
Unit Price: used when shopping
Proportion: a relationship that two ratios or two rates are equal
Two Term Ratio: compares two quantities measured in the same units
Three Term Ratio: compares three quantities measured in the same units
Part to Part Ratio: compares different parts of a group to each other
Part to Whole Ratio: compares on part of a group to the whole group
Unit Rate: a rate in which the second term is one
Unit Price: used when shopping
Proportion: a relationship that two ratios or two rates are equal
Jennily's Seasame street video
Group Member: Jennily, Krizna
Rate: Compare two quantities measured in the same units
Two term Ratio: Compares two quantities measured in the same units
Three term Ratio: Compares three quantities measured in the same units
Part to Part Ratio: Compares different parts of a group to each other
Part to Whole Ratio: Compares on part of a group to the whole group
Unit Rate: A rate in which the second term is one
Unit Price: Used when shopping
Proportion: A relationship that two ratios or two rates are equal
Rate: Compare two quantities measured in the same units
Two term Ratio: Compares two quantities measured in the same units
Three term Ratio: Compares three quantities measured in the same units
Part to Part Ratio: Compares different parts of a group to each other
Part to Whole Ratio: Compares on part of a group to the whole group
Unit Rate: A rate in which the second term is one
Unit Price: Used when shopping
Proportion: A relationship that two ratios or two rates are equal
Sesame Street final post
Part 1
Two Term Ratio: compares 2 quantities measured in the same units.
ex.
or 1:2 or 1/2 or 1 to 2
Three Term Ratio: compares three quantities measured in the same units.
ex.
or 1:2:3 or 1 to 2 to 3
Part to Part Ratio: compares different parts of a group to each other.
ex. 1:1 or 1 to 1
Part to Whole Ratio: compares one part of a group to the whole group.
ex.
1/2 or 50% or 0.5 - A part to whole ratio can be written as a fraction, a decimal, and a percent.
ates: compares two quantities measured in different units.
ex.
$2.00 per 10g or $2.00/10g- rates can be used when buying food.
Unit Rate- a rate in which the second term is one.
ex.
20km an hour or 20km/hr
Unit Price- a unit rate used when shopping.
ex.
per 100g or per 100ml
Proportion- a relationship that says that two ratios or two rates are equal.
ex.
Two Term Ratio: compares 2 quantities measured in the same units.
ex.
or 1:2 or 1/2 or 1 to 2
Three Term Ratio: compares three quantities measured in the same units.
ex.
or 1:2:3 or 1 to 2 to 3
Part to Part Ratio: compares different parts of a group to each other.
ex. 1:1 or 1 to 1
Part to Whole Ratio: compares one part of a group to the whole group.
ex.
1/2 or 50% or 0.5 - A part to whole ratio can be written as a fraction, a decimal, and a percent.
ates: compares two quantities measured in different units.
ex.
$2.00 per 10g or $2.00/10g- rates can be used when buying food.
Unit Rate- a rate in which the second term is one.
ex.
20km an hour or 20km/hr
Unit Price- a unit rate used when shopping.
ex.
per 100g or per 100ml
Proportion- a relationship that says that two ratios or two rates are equal.
ex.
Joshua's Sesame Street Video Post
Group Members: Joshua, Jomer, Breanna
Rate: compares two quantities measured in the same units
Two Term Ratio: compares two quantities measured in the same units
Three Term Ratio: compares three quantities measured in the same units
Part to Part Ratio: compares different parts of a group to each other
Part to Whole Ratio: compares on part of a group to the whole group
Unit Rate: a rate in which the second term is one
Unit Price: used when shopping
Proportion: a relationship that two ratios or two rates are equal
This is our video:
This is the real video:
Rate: compares two quantities measured in the same units
Two Term Ratio: compares two quantities measured in the same units
Three Term Ratio: compares three quantities measured in the same units
Part to Part Ratio: compares different parts of a group to each other
Part to Whole Ratio: compares on part of a group to the whole group
Unit Rate: a rate in which the second term is one
Unit Price: used when shopping
Proportion: a relationship that two ratios or two rates are equal
This is our video:
This is the real video:
Sesame Street Video
Group Members: Samara, Sophia, Krizna, and Jennily
Rate: Compares two quantities measured in the same units.
Two Term Ratios: Compares two quantities measured in the same units.
Three Term Ratios:Compares three quantities measured in the same units.
Unit Price -> a unit rate used when shopping.
Unit Rate ->a rate in which the second term is 1.
Part to whole: a whole ratio can be written as a fraction, a decimal, and a percent.
Part to Part ratio: Compares different part of a group to a whole group.
Rate: Compares two quantities measured in the same units.
Two Term Ratios: Compares two quantities measured in the same units.
Three Term Ratios:Compares three quantities measured in the same units.
Unit Price -> a unit rate used when shopping.
Unit Rate ->a rate in which the second term is 1.
Part to whole: a whole ratio can be written as a fraction, a decimal, and a percent.
Part to Part ratio: Compares different part of a group to a whole group.
Krizna' Profile
Hi,my name is Krizna .I am i a student in grade 8.So if someone were to ask me if I liked math I would say sure.Math isn't a subject that i really like but i think its okay.Its not one of my strongest subjects but I don't mind it.the grade that i had the strongest in math was grade 4.Because in grade 4 i used to love doing division.Because i was really good at it.but I think math is okay.
On grade 7 i really liked doing problem solving I,really liked figuring out problems and playing with numbers.But sometimes when its like a multiplying kind of one its kind of hard.Last year was okay I got almost all of my work done.But I think I did well.
I know already that in grade 8 its just going to get harder But I'm looking forward to doing square roots.And i am looking forward to math n grade 9.
I didn't do a post last year because i never got the chance.But I was disappointed because i didn't do one and it was my on fault i got a bad mark.But this year i will try harder to do more posts and get better marks.
On grade 7 i really liked doing problem solving I,really liked figuring out problems and playing with numbers.But sometimes when its like a multiplying kind of one its kind of hard.Last year was okay I got almost all of my work done.But I think I did well.
I know already that in grade 8 its just going to get harder But I'm looking forward to doing square roots.And i am looking forward to math n grade 9.
I didn't do a post last year because i never got the chance.But I was disappointed because i didn't do one and it was my on fault i got a bad mark.But this year i will try harder to do more posts and get better marks.
Samara's Seasome Street video post
Group Members : Samara and Jennily
Rate: Compares two quantities measured by different units.
Two Team Ratios: Compares two quantities measured in the same units.
Three Team Ratios : Compares three quantities measured in the same units.
Unit Rates: A rate in which the second team is 1.
Unit Price: A unit rate used when shopping.
Part to Part ratio: Compares different part of a ratio to each other.
Part to Whole Ratio: Compares one part of a group to a whole group.
Proportional Reasoning: A relationship that says that two rations are equal.
Rate: Compares two quantities measured by different units.
Two Team Ratios: Compares two quantities measured in the same units.
Three Team Ratios : Compares three quantities measured in the same units.
Unit Rates: A rate in which the second team is 1.
Unit Price: A unit rate used when shopping.
Part to Part ratio: Compares different part of a ratio to each other.
Part to Whole Ratio: Compares one part of a group to a whole group.
Proportional Reasoning: A relationship that says that two rations are equal.
Part 1:
Two Term Ratio - a two term ratio compares two quantities that are measured in the same unit.
Example: 3:4 or 3 to 4.
Three Term Ratio - a three term ratio compares three quantities that are measured in the same units
Example: 3:4:5 or 3 to 4 to 5
Rate - a rate compares two quantities measured in different units.
Like $0.20 / apple or $10.00/g ( like when your shopping )
Unit Rate - a rate in which the 2nd term is one.
For example 15ms / second or 100ms / min
Unit Price - a rate used when shopping
Examples: per 100gs, per 50mls
Proportional Reasoning (P.R) - a relationship that says two ratios or two rates are equal.
For example: 2/3 = 4/6
Part 2:
The video we based ours on was:
Professor Grover teaches the class about "School" but he gets EVERYTHING wrong and the kids have to correct him.
Part 3:
Our video!
Two Term Ratio - a two term ratio compares two quantities that are measured in the same unit.
Example: 3:4 or 3 to 4.
Three Term Ratio - a three term ratio compares three quantities that are measured in the same units
Example: 3:4:5 or 3 to 4 to 5
Rate - a rate compares two quantities measured in different units.
Like $0.20 / apple or $10.00/g ( like when your shopping )
Unit Rate - a rate in which the 2nd term is one.
For example 15ms / second or 100ms / min
Unit Price - a rate used when shopping
Examples: per 100gs, per 50mls
Proportional Reasoning (P.R) - a relationship that says two ratios or two rates are equal.
For example: 2/3 = 4/6
Part 2:
The video we based ours on was:
Professor Grover teaches the class about "School" but he gets EVERYTHING wrong and the kids have to correct him.
Part 3:
Our video!
Thursday, October 28, 2010
Prime Factorizaton and Square Roots
Show You Know: (page 82)
Write the prime factorization of each number. Which number is not a perfect square? Explain how you know.
prime factorization- a number written as the product of its prime factors.
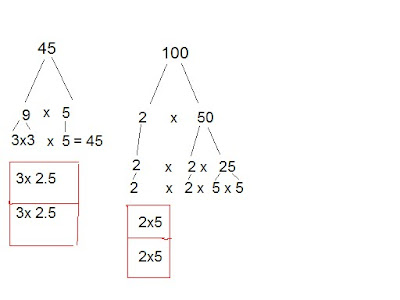
Write the prime factorization of each number. Which number is not a perfect square? Explain how you know.
prime factorization- a number written as the product of its prime factors.

45 is not a perfect square.
Textbook Questions: 1, 5, 10, 15 (pg. 85 & 86)
1.) Explain how to square the number 7.
answer: To square the number 7 you multiply 7x7=49.
5.)a.) Determine the prime factorization of 4.
b.) Is 4 a perfect square? Explain.
c.) Draw the square and label its side length.
answers:
a.) The prime factorization of 4 is 2x2=4
b.) 4 is a perfect square because its square root is a whole number with no decimals. ( 4's square root is 2)
10.) Determine the area of a square with each side length.
a.)20
b.)17
answers:
a.) area: s x s= s squared
20 x 20= s squared
20 x 20= 400 square units
b.) area: s x s= s squared
17 x 17= s squared
17 x 17= 289 square units
16.) Determine the value.
a.) square root of 9.
b.) square root of 25.
c.) square root of 1600.
answers:
a.) The square root of 9 is 3. (3x3=9)
b.) The square root of 25 is 5. (5x5=25)
c.) The square root of 1600 is 40. (40x40=1600)
Wednesday, October 27, 2010
Ryan's Math Profile
Hi my name is Ryan Mercado. I am a math student in grade 8. If someone asked me do you like math? I would say yes becauase math is important in life. I say this because when you get older and you buy things by yourself you need to know how much money you need to pay for something. The best thing i did last year was blogging because it was fun and you can help people when they need it. Also i think of it as test to see if I pay attention in class.
In grade 7 my favorite unit was fractions because i already knew some things about it. I did well in this unit becauase I knew what I was doing for the entire unit and if i had to I would explain how i got an answer. The unit i didnt do well in last year was the co-ordinate grid. I knew the basic things that you had to do but i got confused about the three transformations except for rotation. This year i must pay attention in class so I know what do in a unit.
This year in grade 8 i will try to help my classmates with things they dont get so they can get it and do the rest of the work with no help. I also wanna make more blogs because it will test me if I payed attention in class or not. This year I would like to learn more about algebra because im weak at it so I wanna try to improve on it so I dont have to always ask what do we do or i dont
get it.
Last year I did a blog about Why We Estimate because I wanted to help people who didnt get the unit. Blogging helped me get better because when i dont get something I can look at the blog and try to find out what i dont get. When were on computers in math class I hope to do more blogs and make sure I get homework done on time.
In grade 7 my favorite unit was fractions because i already knew some things about it. I did well in this unit becauase I knew what I was doing for the entire unit and if i had to I would explain how i got an answer. The unit i didnt do well in last year was the co-ordinate grid. I knew the basic things that you had to do but i got confused about the three transformations except for rotation. This year i must pay attention in class so I know what do in a unit.
This year in grade 8 i will try to help my classmates with things they dont get so they can get it and do the rest of the work with no help. I also wanna make more blogs because it will test me if I payed attention in class or not. This year I would like to learn more about algebra because im weak at it so I wanna try to improve on it so I dont have to always ask what do we do or i dont
get it.
Last year I did a blog about Why We Estimate because I wanted to help people who didnt get the unit. Blogging helped me get better because when i dont get something I can look at the blog and try to find out what i dont get. When were on computers in math class I hope to do more blogs and make sure I get homework done on time.
Ryan's Sesame Street Video Post
Group members: Ryan M, Christian T, Kris G .
Part One
Two/Three term ratios- Compares two/three quantities measured in the same unit.
Example: 5 oranges, 2 grapes. 5:2
5 oranges, 2 grapes, to all. 5:2:7
Rates- Compares 2 quantities measured in different units.
Example: 10g= 1.50$/10g
Proportional Reasoning- A relationship that says 2 ratios and 2 rates are equal.
$/g 5$/5g= 10$/10g
x2
Part Two
My group and I did a remake of the Sesame Street Video called The Scale Salesman
It's about left trying to sell Ernie a scale.
Part Three
Want to buy a proportional reasoning?
Part One
Two/Three term ratios- Compares two/three quantities measured in the same unit.
Example: 5 oranges, 2 grapes. 5:2
5 oranges, 2 grapes, to all. 5:2:7
Rates- Compares 2 quantities measured in different units.
Example: 10g= 1.50$/10g
Proportional Reasoning- A relationship that says 2 ratios and 2 rates are equal.
$/g 5$/5g= 10$/10g
x2
Part Two
My group and I did a remake of the Sesame Street Video called The Scale Salesman
It's about left trying to sell Ernie a scale.
Part Three
Want to buy a proportional reasoning?
Labels:
"Sesame Street Video",
ratiorateproportion,
Ryan8-73
Tuesday, October 26, 2010
Jomer's Scribe On Square Roots
Square Roots
We were learning about square numbers.. and now we're learning about square roots


We were learning about square numbers.. and now we're learning about square roots


Heres a Link to help you understand more about squares and square roots.
Monday, October 25, 2010
Karl's Perfect Square Post
An example of a perfect square is:
1x1, 2x2, 3x3 or it could be written 1², 2², 3².
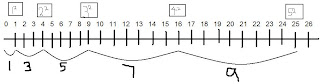
If you noticed, the intervals in between each perfect square is an odd number.
HOMEWORK:
-You Have to finish your Number Line.
- Tell what you know about these squares :
[1] [2] [3] [4] [5] [6] [7] [8] [9]
Here is a video about square roots.
Here is a link to a page that helps you with square roots.
1x1, 2x2, 3x3 or it could be written 1², 2², 3².

If you noticed, the intervals in between each perfect square is an odd number.
HOMEWORK:
-You Have to finish your Number Line.
- Tell what you know about these squares :
[1] [2] [3] [4] [5] [6] [7] [8] [9]
Here is a video about square roots.
Here is a link to a page that helps you with square roots.
Sunday, October 24, 2010
Meldrick's Square Numbers Post
Square Numbers and Square Roots
Focus On
Focus On
- determine the square of a whole number
- determine the square root of a perfect square
- is the product of the same two numbers; 3 x 3 = 9, so 9 is a square number.
- is also known as a perfect square; a number that is not a perfect square is called a non perfect square.
Homework:
- the perfect square chart
That is all... remember to comment!
Tuesday, October 19, 2010
Sophia's math profile
Hi my name is Sophia well most of you call me Sophie. I am a grade 8 student and my worst subject is math. I think it's because math is hard for me but maybe it's really because I don't try hard enough. Not everything in math is hard for me. In the beginning of chapter 2 there was ratio charts it was so easy I could do it for the whole year. But then there's proportions which I never really got(can any of you help me). MULTIPLYING. I do really poorly at it and in math support Mr.Harbeck taught us how to play a game that he did when he was in grade 4 everday at lunch time him and his mother would play the game so he could get better at it and I'm doing that same thing because it is one of the things that will make me a better student. I have so many goals for math because it's not just to pass grades it's for the future. You need to know and remember how to do everything you've done in school. Cause everywhere you go there is math. Same with reading, remember when you where younger you were just learning how to read( you thought it was hard but you're parents made you try harder)right. Well that's the same with math. Soon all of us will be so good in math we won't even remember that we struggled. All of us will be good at different times. Another goal is to keep and review every test I have done so when we have exams I know exactly what to do. Another one is to listen in class closely and take down notes for the stuff I don't know so I can get help on it later. When I was younger and I mean back in grade 3 I was one of the poorest math people in my class ever. But when it came to number lines. NUMBER LINES where my favourite(so fun:) wanna know why. Because we wold be in a group of 5 or 6 and then we would use licorise for the numer line and play diffrent number line games. My favourite part is the treats. Another thing we did in grade 3 was playing multyplying games and Math bingo. (so fun:). When it comes to math games I'm a pro cause all I think about it is winning. The same with vollybal(to me). When I'm practising without a ball it is so easy and I mean EASY. But when we are actually playing a game WITH THE BALL that's all I think about yes that's all I think about, the ball.
Monday, October 18, 2010
Oliva's seseme street vedio
Two Term Ratio: Compares two quantities measured in the same units.
Tree Term Ratio: Compares three quantities measured in the same units.
Rate: Compares two quantities measured in different units.
Unit Rate: A rate witch the second term is one.
Unit Rate: A unit rate used when shopping.
Proportion: A relationship that says that two ratios or two rates are equal.
Script for ``Kermit and cookie monster and the mystery box
Kermit- standing around with the clue box
Cookie Monster- walks in
Cookie Monster- cookie want cookie
Kermit- no cookie for you
Kermit- cookie monster would you like to play a guessing game
Cookie Monster- want cookie
Kermit- no cookie
Cookie Monster- no cookie no guessing game
Kermit- if you guess whats in the box you can have a cookie
Cookie Monster- guesses randomly horse, dog, fish, diamond, cake, cat
Kermit- those are wild guesses
Cookie Monster- me wild about cookies
Kermit- listen to the clues
Cookie Monster- me all ears
Kermit- the first clue is that it is very helpful when you need to find a price
Cookie Monster- is it a cookie
Kermit- no its not a cookie
Cookie Monster- not a cookie
Kermit- the second clue is that it compares two quantities measured in different units
Cookie Monster- is it a cookie
Kermit- no its not a cookie
Kermit- the third clue is...........
Cookie Monster- just thought it might be cookie off chance
Kermit- no its not a cookie
Kermit- OK the third clue is that it is a math term
Cookie Monster- it helps you find the price
Kermit- um hum
Cookie Monster- it compares two quantities measured in different units and it is a math term...................... is it a...... cookie
Kermit- no its not a cookie
Cookie Monster- thought one last chance
Kermit- no its not a cookie
Cookie Monster- me give up
Kermit- how can you give up it helps find the price, it compares two quantities measured in different units, and it is a math term. ITS A RATE!!!!!, A RATE!!!!!!
Cookie Monster- like that forth clue is it a rate
Kermit- of coarse its a rate i just told you it was a rate
Cookie Monster- me guess right me get cookie
Cookie Monster- give me cookie
Kermit- i told you what it was you didn't guess it right
Cookie Monster- Kermit you know life not all guessing game frog sometimes we have to care about Friends especially Friends who love cookies so much that they play silly guessing games because maybe just maybe a very handsome frog who has cookie will give best best Friend who can not live without cookie give that best Friend cookie but if you not Friend then.............
Kermit- OK OK you can have a cookie
Cookie Monster- one measly cookie speech like that deserve more cookies
Kermit- i only have one cookie
Cookie Monster- oh that's OK um um um chomp chomp
Tree Term Ratio: Compares three quantities measured in the same units.
Rate: Compares two quantities measured in different units.
Unit Rate: A rate witch the second term is one.
Unit Rate: A unit rate used when shopping.
Proportion: A relationship that says that two ratios or two rates are equal.
Script for ``Kermit and cookie monster and the mystery box
Kermit- standing around with the clue box
Cookie Monster- walks in
Cookie Monster- cookie want cookie
Kermit- no cookie for you
Kermit- cookie monster would you like to play a guessing game
Cookie Monster- want cookie
Kermit- no cookie
Cookie Monster- no cookie no guessing game
Kermit- if you guess whats in the box you can have a cookie
Cookie Monster- guesses randomly horse, dog, fish, diamond, cake, cat
Kermit- those are wild guesses
Cookie Monster- me wild about cookies
Kermit- listen to the clues
Cookie Monster- me all ears
Kermit- the first clue is that it is very helpful when you need to find a price
Cookie Monster- is it a cookie
Kermit- no its not a cookie
Cookie Monster- not a cookie
Kermit- the second clue is that it compares two quantities measured in different units
Cookie Monster- is it a cookie
Kermit- no its not a cookie
Kermit- the third clue is...........
Cookie Monster- just thought it might be cookie off chance
Kermit- no its not a cookie
Kermit- OK the third clue is that it is a math term
Cookie Monster- it helps you find the price
Kermit- um hum
Cookie Monster- it compares two quantities measured in different units and it is a math term...................... is it a...... cookie
Kermit- no its not a cookie
Cookie Monster- thought one last chance
Kermit- no its not a cookie
Cookie Monster- me give up
Kermit- how can you give up it helps find the price, it compares two quantities measured in different units, and it is a math term. ITS A RATE!!!!!, A RATE!!!!!!
Cookie Monster- like that forth clue is it a rate
Kermit- of coarse its a rate i just told you it was a rate
Cookie Monster- me guess right me get cookie
Cookie Monster- give me cookie
Kermit- i told you what it was you didn't guess it right
Cookie Monster- Kermit you know life not all guessing game frog sometimes we have to care about Friends especially Friends who love cookies so much that they play silly guessing games because maybe just maybe a very handsome frog who has cookie will give best best Friend who can not live without cookie give that best Friend cookie but if you not Friend then.............
Kermit- OK OK you can have a cookie
Cookie Monster- one measly cookie speech like that deserve more cookies
Kermit- i only have one cookie
Cookie Monster- oh that's OK um um um chomp chomp
Karl's Sesame Street Video Post
Group members : Louis D, Karl N, Chris A.
Part 1
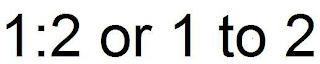
Three-Term Ratio : compares three quantities measured in the same unit ex.
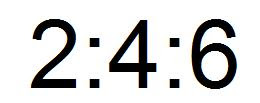
Rate : compares two quantities measured in different units.
ex.
$1.00 per g or $1.00/g
Unit Rate : a rate in which the second term is one.
ex.
72 words typed in a minute or 72 words/min.
Unit Price : a unit rate used when shopping.
ex.
$1.00 per g or $1.00/g
Proportional Reasoning : a relationship that says to ratios are equal.
ex.

Part 2
Part 3
Part 1
Two-Term Ratio : compares two quantities measured in the same unit.
ex.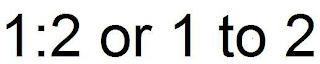
Three-Term Ratio : compares three quantities measured in the same unit ex.
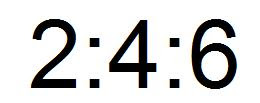
Rate : compares two quantities measured in different units.
ex.
$1.00 per g or $1.00/g
Unit Rate : a rate in which the second term is one.
ex.
72 words typed in a minute or 72 words/min.
Unit Price : a unit rate used when shopping.
ex.
$1.00 per g or $1.00/g
Proportional Reasoning : a relationship that says to ratios are equal.
ex.

Part 2
Part 3
Maya's Sesame Street Post
Group members - Me, Meldrick and Ana.
Me as Zoe.
Ana as Elmo.
Meldrick as Alfred.
Me as Zoe.
Ana as Elmo.
Meldrick as Alfred.
RATIOS -
Two term ratios - Compares two quantities in the same units.
Part to whole ratio - Compares one part of a group to the whole group.
Three term ratios - Compares three quantities measured in the same units.
Part to part ratio - Compares different parts of a group to each other.
Three term ratios - Compares three quantities measured in the same units.
Part to part ratio - Compares different parts of a group to each other.
* A part to whole ratio can be written as a fraction, a decimal, and a percent.

Here's the link to the actual video.
Heeeeeeeere!
Heeeeeeeere!
Ana Lopena's Sesame Street video
Group members- Ana Lopena, Maya Ladesma and Meldick A.




RATIOS- compares 2 or more quantities measured in the same unit
two-term ratio- compares 2 quantities measured in the same unit
three-term ratio- compares 3 quantities measured in the same unit
part to part ratio- compares different parts of a group to each other
part to whole ratio- compares part of the group to the whole group

RATES- compares 2 quantities measured in different units
unit rate- a rate in which the second term is 1
unit price- a unit rate used when shopping
PROPORTIONAL REASONING- a relationship that says that two

ratios or rates are equal
This is our video about how to make a ratio. ENJOY!!
THIS IS THE REAL VIDEO <-----
Louis' Sesame Street Video Post
Group members: Chris A, Karl N, Louis D
Two-Term Ratio : compares two quantities measured in the same unit.
ex.


Three-Term Ratio : compares three quantities measured in the same units.
ex.

Rates : compares two quantities measured in different units.
ex.
$3.00 per 20g or $3.oo/20g (can be used in shopping)
Unit Rate : a rate in which the second term is one
ex.
75 words typed in one minute or 75 words/minute
Unit Price : a unit rate used when shopping
ex.
per 100g or per 100ml
Proportional Reasoning : a relationship that says two ratios or two rates are equal
ex.
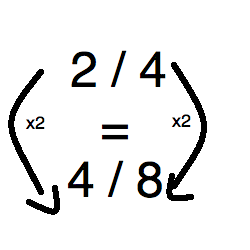
Part 2
Professor Grover teaches a class on school. He gets facts about school wrong and the children have to correct him all the time.
Part 3
Labels:
"Sesame Street Video",
Louis873,
ratiorateproportion
Kris' Sesame Street Video
GROUP MEMBER
Kris G, Christian T and Ryan M
RATIO
Two Term Ratio - Compare two quantities measured in the same unit.
Three Ratio Term - Compare three quantities measured in the same unit.
EG for two term ratio.
6 HATS:4 SHIRTS
6:4
 for three term ratio.
for three term ratio.
6 HATS:4 SHIRTS:TOTAL
6:4:10
RATE
Compare two quantities measured in different unit's.
EG for rate
400/KM
Proportional
A relation that says two ratio's and two rate's are equal.
EG for porportional
money $4 - $16
------- ---- -----
shirts 2 - 8
OUR POST
Kris G, Christian T and Ryan M
RATIO
Two Term Ratio - Compare two quantities measured in the same unit.
Three Ratio Term - Compare three quantities measured in the same unit.

EG for two term ratio.
6 HATS:4 SHIRTS
6:4
 for three term ratio.
for three term ratio.6 HATS:4 SHIRTS:TOTAL
6:4:10
RATE
Compare two quantities measured in different unit's.
EG for rate
400/KM
Proportional
A relation that says two ratio's and two rate's are equal.
EG for porportional
money $4 - $16
------- ---- -----
shirts 2 - 8
OUR POST
Subscribe to:
Posts (Atom)

